All of the previously discussed design storms were developed from rainfall frequency- duration relationships or from observations of rain gauge records, they did not use a statistical procedure to analyze the historical rainfall record. Yen and Chow (1980) use the method of moments to statistically determine the geometry of hyetograph. Using a triangular hyetograph representation, only the first moment is required to determine the location of the hyetograph peak.
Rainstorms are analyzed to determine the average depth per time interval
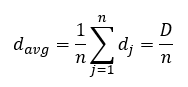
and the first moment arm of the hyetograph
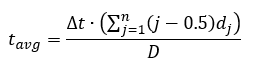
where:
n = number of intervals in the storm,
= rainfall depth in interval j,
D = total storm depth,
= average storm depth,
t = time step of each interval,
= average storm duration.
To describe the hyetograph in more general terms, the hyetograph is non-dimensionalized using D, the storm depth, and td, the storm duration. The non-dimensionalized form of these two equations can be expressed in the following two forms:
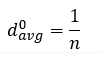
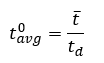
where:
= non-dimensional average storm depth,
=non-dimensional average storm duration.
The hyetograph is described with geometric variables a, b and h. In a non-dimensionalized form, the variables are expressed by:
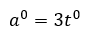
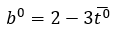
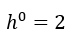
The historical rainfall record is then analyzed to determine values for a, b, h for 6 particular localities. Yen and Chow have only done this for a rainfall record from Illinois and from Boston. Once the design storm non-dimensionalized variables are determined, the design storm can be developed. After selecting the duration and return period, the rainfall depth is found from an IDF curve. Using the non-dimensionalized variables for the area the design storm is constructed.
The Yen and Chow design storm requires a rainfall data analysis before it can be used in a particular locality. The non-dimensionalized variable a, can only be found by analyzing a local rainfall record. It should, not be transported from one locality to another.


