WILHYD is the subroutine that uses the unit hydrograph proposed by Williams and Hann (1973). The unit hydrograph is divided into three parts for computation. The first part, from the beginning of rise to the inflection point, , is computed by the 2-parameter gamma distribution equation (Equation 18). The second part from the inflection point,
to
where
=
+ 2_K_, is computed by
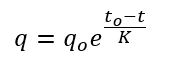
The third part from onwards is computed by
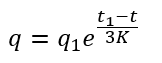
n is computed as a function of K/ and
is a function of n and
. Therefore only 2 parameters, K and
are necessary to compute the entire unit hydrograph. Empirical relations have been derived for K and
(Williams 1977) based on Southern U.S. watersheds. These relations may not be applicable in other areas.
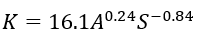
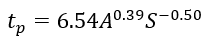
where:
K = the recession constant (hr);
= the time to peak (hr);
A = the watershed area (sq. miles); and
S = the difference in elevation in feet, divided by flood plain distance in miles, between watershed outlet and most distant point on the watershed.
The unit hydrograph in WILHYD has a longer recession tail than that in NASHYD and a smaller peak. It can therefore be used in those watersheds where the recession limb is longer.
A comparison of the two-unit hydrographs is shown in the figure below.
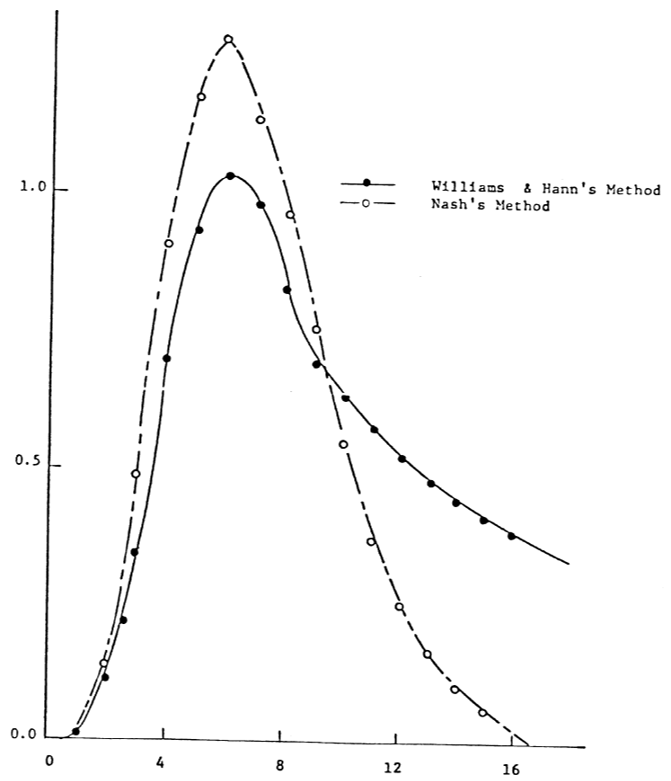
COMPARISON OF UNIT HYDROGRAPH BY: (I) WILLIAM’S AND HANN’S METHOD (II) NASH’S METHOD


