Many ways of deriving synthetic unit hydrographs or IUH have been proposed since the early studies of Snyder in 1938. One frequently used way is by means of a conceptual model made up of a cascade of equal, linear reservoirs, first proposed by Nash in 1957. The IUH for Nash’s model can be written as:
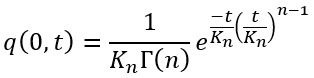
where:
Γ(n) = the gamma function;
n = the number of reservoirs;
= the storage coefficient of each reservoir.
By differentiating Equation 15 with respect to t/ and equating to zero, the time to peak
in terms of n and
is obtained.
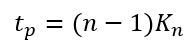
The peak flow then becomes
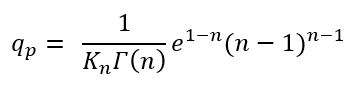
By substituting Equations 16 and 17 in Equation 15, the 2-parameter gamma equation is obtained
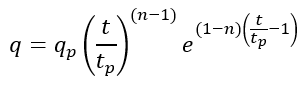
Williams and Hann (1973) use this equation from the time of rise to the inflection point for the IUH in WILHYD. Figure 19 shows the variation of the outflow hydrograph from NASHYD, with the number of reservoirs, n, for a fixed time to peak.
As shown in the figure below, for the same time to peak, the peak flow is sensitive to n in the range 2 to 6. The parameter n, can be a non-integer. The calibration of watersheds with areas of less than 15 on the Seymaz and Etobicoke studies presented in the previous section has shown that a first estimate for N = 3 can be used if data is unavailable. For consistency, the various subwatersheds should use the same n unless data is available for each subwatershed.
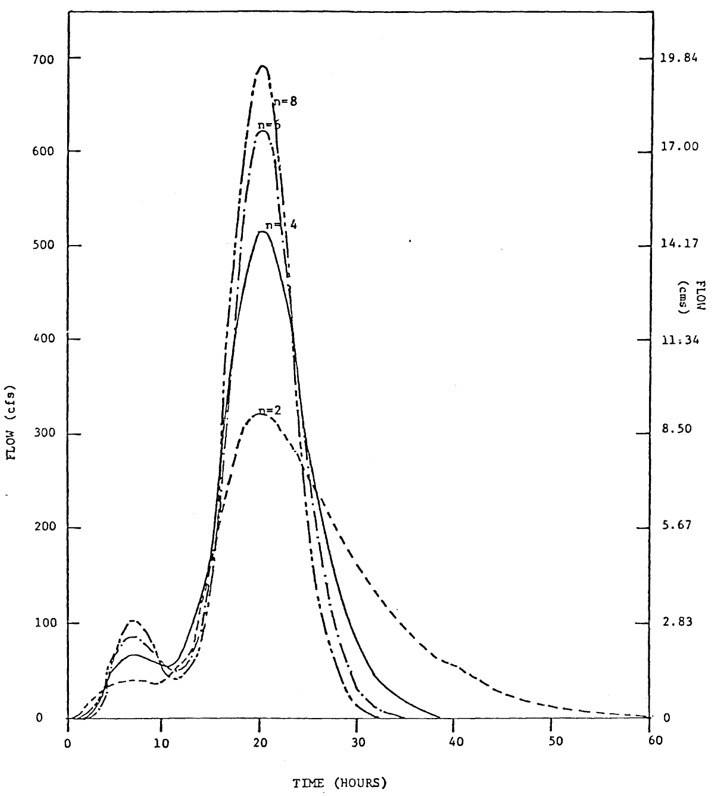
VARIATION OF HYDROGRAPH (NASHYD) WITH THE NUMBER OF RESERVOIRS (N) FOR FIXED


