For pervious areas, there are two options for calculating the infiltration losses. The first option is Horton’s equation where the infiltration capacity rate is an exponential function of time, which decays to a constant rate. It is written as follows:
(4)
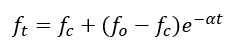
where:
= the infiltration capacity rate (in/hr or mm/hr) at time t;
= the initial infiltration capacity rate (in/hr or mm/hr);
= the final infiltration capacity rate (in/hr or mm/hr);
= the decay rate (1/hr).
The equation is only satisfactory for the condition that the rainfall intensity is higher than the infiltration capacity rate. To overcome this problem, the cumulative form of the equation can be used. It has the advantage that the infiltration rate becomes a function of the amount of water accumulated into the soil.
(10)
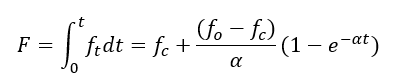
where F is the cumulative infiltration volume, at time t.
The average infiltration capacity rate during the next time step is
(11)
In order to determine the actual infiltration rate f, the average infiltration capacity rate is then compared with the average rainfall intensity i during the time period ∆t.
If
(12)
then the calculation proceeds to the next time step with the cumulative infiltration volume at 
. If f = i, then the actual cumulative infiltration would be
(13)
where
(14)
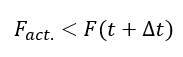
The new time 
, which would correspond to the cumulative infiltration 
, is determined by means of an iterative process. The calculation then continues from this point for the next time step.
The antecedent moisture condition can be represented by the water, F, accumulated into the soil before the start of the storm. F can be directly specified as input. The other infiltration parameters also need to be specified.
For a decay rate of 4.0 
the infiltration capacity rate declines 98% towards the limiting value after 1 hour (if the rainfall intensity is always higher than the infiltration capacity rate). For α = 2.0 , the decline is 76% after 1 hour. This should be considered when selecting the time increment ∆t for computation.
