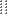A rain garden receives flow from its drainage area and retains surface runoff. The ponding water is promoted to infiltrate into engineering soil layer based on hydraulic conductivity and permeability of various soil types. The rate of infiltration occurring at the bottom of the surface layer is calculated following the same steps as those developed for the soakaway, chamber and pavement (Equations (10.1) and (10.2)). Similarly, the overflow and percolation processes in a rain garden are calculated using those equations used for the LIDs. Evaporation (
)occurs from the surface of detention water, and percolation of the stored water to the engineering soils continues. Once the storage is empty, evapotranspiration may still happen on the engineering soil surface until soil water content of the engineering soil is empty. Finally, the volume of water content in the engineering soil layer (
) is updated using the continuity equation (Equation (10.33) (m³)), and the amount of the percolated water is added to soil water content of the native soil. The figure below illustrates a typical hydrology of a rain garden system.
SCHEMATIC DIAGRAM OF A RAIN GARDEN FACILITY AND ITS HYDRAULIC PATTERN
(10.32)
(10.33)
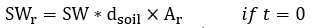
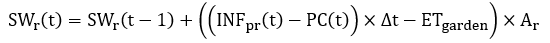
In the rain garden, the calculation of ponding storage capacity is the same steps as pavement (Equation 10.25). When the surface ponding storage is filled with water, any runoff from upstream bypasses the rain garden. The summation of the bypassing runoff becomes the total surface runoff. The amount of water stored in the surface ponding storage of a rain garden is calculated using a continuity equation:
(10.34)
(10.35)
(10.36)
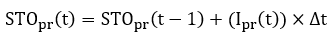
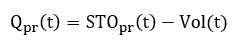
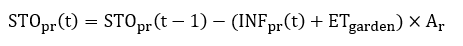
Where 
is volume of water in a ponding layer (m³) during the time step t; Ic is the inflow to the rain garden (m³). INFpr, which is constant (m/s) in a single event t or continuous simulations or using Green-Ampt Mein-Larson (GAML) equation to calculate infiltration in a continuous model. Ar is the bottom area of rain garden (m²). Surface runoff would be calculated if volume of ponding water () exceeds the ponding storage capacity (Vol(t)).
