In the chamber model, infiltration, outflow overflow and underdrain flow are the main process involved with underground chamber (see the figure below). Users could calculate Infiltration rate by using the Green-Ampt Mein-Larson (GAML) equation ((Equations (10.1) and (10.2)) or a constant rate in a continuous model and only a constant infiltrate rate in single event model. Overflow would be generated if volume of water stored is larger than the volume of chamber (Equations (10.19)). Orifice is the underdrain flow rate (m³/s) and calculated by depth discharge curve or orifice equation. Outflow flow rate is calculated by using discharge (i.e. outflow) and storage rating curve. A discharge-stage (storage) relationship defines the relationship between discharge (m³/s) and the depth of water (storage volume) in the storage facility. The discharge can be calculated by using simple geometric formulas expressed as a function of depth of water (volume of storage). After the required discharge has been estimated, the configuration of the depth (storage) must be determined so that the stage (storage)-discharge curve can be developed.

UNDERGROUND CHAMBER MODEL SCHEMATIC
In chamber storage layer, continuity equations can be written as follows:
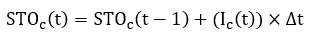
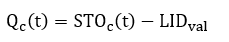
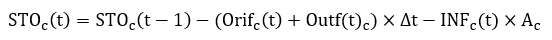
where is volume of water stored in a chamber (m³) during the time step t;
is the inflow rate from the contributing catchment (m³/s);
is the infiltration rate (m/s), which is constant (m/s) in a single even t and using a constant rate or Green-Ampt Mein-Larson (GAML) equation to calculate infiltration in a continuous model;
is water surface area (m²);
(t) and
(t) are underdrain flow rate and outflow rate during the time step t.
is the max water stored volume of the chamber and calculated by using a depth-cumulative storage table.
In the native soil layer, a continuity equation is used to account water content of the soil base:

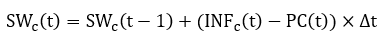
where is soil water content of the soil layer (m) and PC is the percolation rate in the soil base to ground water(m/s).


