Enhanced grass swales are gently sloping vegetated open channels designed to convey and treat stormwater runoff. They are designed with limited longitudinal slopes to force the flow to be slow and shallow, thus allowing for particulates to settle and limiting the effects of erosion. Berms and/or check dams installed perpendicular to the flow path promote settling and infiltration (see the figure below).
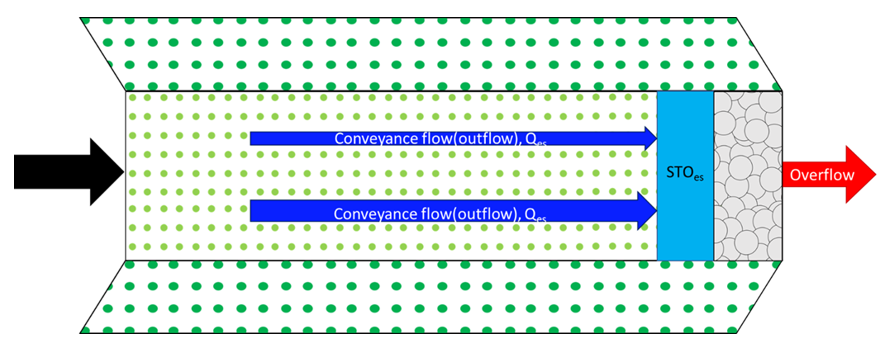
ENHANCED SWALE PLAN VIEW
In VO, the enhanced swale system includes surface ponding and storage layers. In the ponding layer, Manning’s equation (Equation 1.6) is used to calculate the flow capacity () of a swale. This allows the flow rate and flood levels to be determined for variations in swale dimensions, vegetation type and longitudinal grade. If inflow is small than the flow capacity (
), inflow would infiltrate into the storage layer, while inflow would be equal to flow capacity. The water volume stored in the surface ponding layer,
, is given by Eq. (10.47):
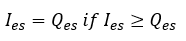
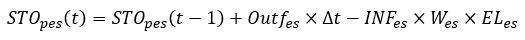
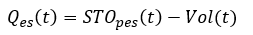
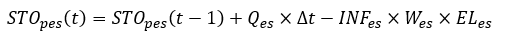
where is volume of water in a surface ponding (m³) during the time step t;
is the outflow calculated by using manning equation (m³/s).
, is permeability (m/s) from swale surface (
) to the storage layer and is determined by users. Wes is width of the swale (m);
is the effective length (m).
In the storage layer, if inflow rate is small than permeability, permeability is equal to inflow rate. The water volume in the storage layer is written by Eq. (10.48). The figure below illustrates a typical hydrology of a rain garden system.
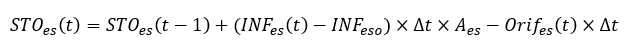
Where is volume of water in a storage layer (m³) during the time step t;
, which is constant (m/s) in a single even t and using Green-Ampt Mein-Larson (GAML) equation to calculate infiltration in a continuous model.
is the bottom area of the swale (m²);
is the underdrain flow (m³/s).
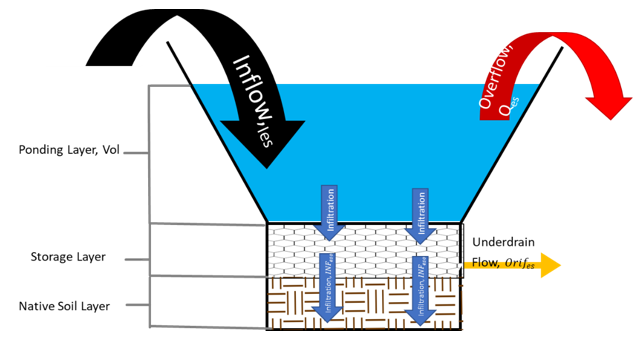
SCHEMATIC DIAGRAM OF AN ENHANCED SWALE