Elliptic Curve Cryptography is a cryptographic system used by most cryptocurrencies and is considered much more secure than modern cryptographic functions, such as RSA.
An elliptic curve is the set of points that satisfy a specific mathematical equation. The equation for an elliptic curve looks something like this:
y2 = x3 + ax + b
The following is an excerpt from Medium.com
This real-world use case of mathematics invigorated the research into more fringe mathematics to find something that would further revolutionize cryptography.
In 1985, cryptography based on elliptic curves was proposed independently by Neal Koblitz and Victor Miller.
Elliptic curves have some curious characteristics that make them useful. They are defined as a completely smooth curve (non-singular), and a line between two points on this curve will always intersect a third point (projective). This allows you to hop around this curve easily (computationally) quickly and procedurally develop an endpoint that has seemingly no relation to the starting point and is very difficult to reverse the path that led you there.

Elliptical curve with points defined as y² = x³ + ax + b
The same ideas of finding two unique numbers (points in a two-dimensional curve) related and a max ceiling to wrap around apply in cryptographic usage.
How do we go about getting two related numbers but in a way that no one can tell? Well, we use the curve’s projective property and draw a line tangent to the starting point P, finding where it intersects the curve at a second point Pʹ. Then flip the axis and draw a line from that new point (2•P) through the starting point and find the new intersection point Pʹʹ. Then flip the axis and draw a line from that new point (3•P) through the starting point and find the new intersection point Pʹʹʹ etc. (this mathematical operation is called point multiplication).
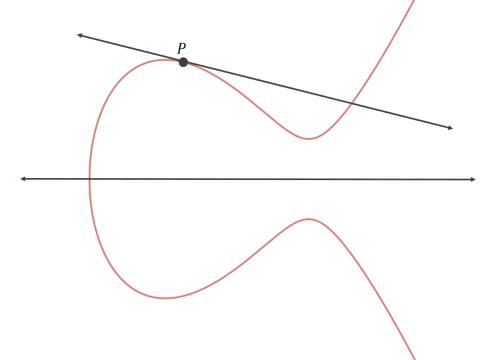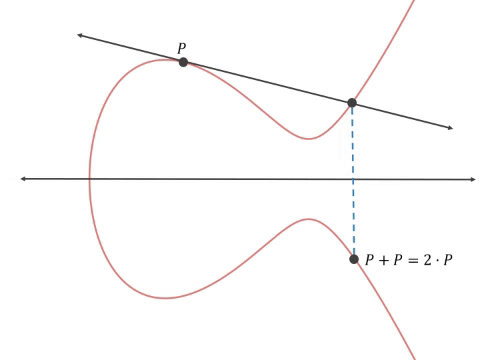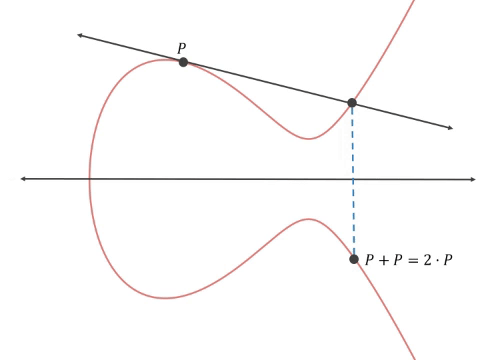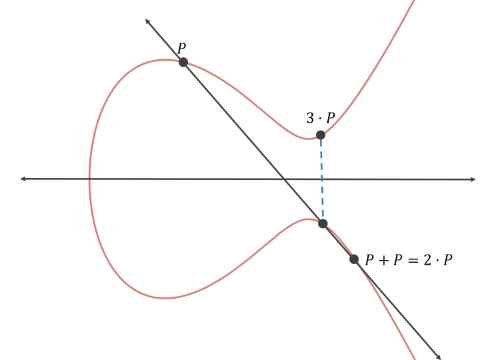
Point multiplication starting with the tangent to point P and ending with point 3•P
We do this n times and end up with a point on the curve, Q, that has no obvious relationship to the starting point and can be defined as Q=n•P, where n is the number of iterations of point multiplication done. Mathematically this works out to Q = P + P + P … n times.
So if you knew the curve we used, the starting point P, and the ending point Q, could you determine n? It turns out there is no known algorithm to do this. No shortcuts in determining how many times you “dotted” P to get to Q. You basically have to keep adding P to itself and count how many times you have to do it to get to Q (or the other way around). This is fairly easy with small n, but what happens when n gets big? and I mean really big…
Elliptic Curves in Application
The elliptic curve used by Bitcoin, Ethereum, and many others is the secp256k1 curve, with an equation of y² = x³+7 and looks like this:

Elliptic curve secp256k1 over real numbers. Note that the real implementation of the curve is over a defined prime field of positive integers and therefore looks nothing like the above.
And has a defined starting point used by all key generation, P(x, y), with x and y coordinates:
x-coordinate: 55066263022277343669578718895168534326250603453777594175500187360389116729240
y-coordinate: 32670510020758816978083085130507043184471273380659243275938904335757337482424
As you can see, with a starting point THAT big, having an ending point larger than the allowed 512-bit key size is possible. We, therefore, have to set a maximum value that we wrap around to establish a field of allowed points that fit our key size.
For this specific curve, the maximum (mod) value is defined by a prime number (to yield a prime field) of:
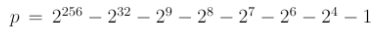
OR
115792089237316195423570985008687907853269984665640564039457584007908834671663
OR
115 quattuorvigintillion …
OR
.12% of all the atoms in the known universe.
So, in the end, your private key is just a large integer, and your public key is a point on the curve corresponding to your private key point multiplied with the starting point.
Let’s try to visualize just how secure this is. If the selection of n was truly random, how long would it take for you to find a specific n, or just in general, any “collision” with another, in-use, private key? Let us say you could try 250 billion possibilities a second, 5 times the current Bitcoin network hash rate, and it would still take 1⁰¹⁰ times the age of the universe to find a match. Basically, anything else happening is more probable than finding a match.
There has been some research done to establish ways of measuring the security of these encryption types. In these scales, ECC in the defined curve and field above is considered “Globally Secure,” meaning the energy a computer or group of computers would have to use to find a specific n would be enough energy to boil 1,400,000,000 km³ of water, which is just about all the water on the surface of the earth. That’s probably secure enough.
Reference:
G. (2018, June 29). Elliptic-Curve Cryptography – Coinmonks – Medium. Retrieved from https://medium.com/coinmonks/elliptic-curve-cryptography-6de8fc748b8b


Post your comment on this topic.