19.2.4 Weighting Functions

Each error source has a set of weighting functions which define how that error source effects the actual survey measurements of measured depth, inclination and azimuth. These weighting functions are simply the equations that link the error source to the survey measurements, e.g. the weighting functions enable us to take a zmagnetometer bias uncertainty in nano-Teslas and calculate a survey azimuth uncertainty in degrees at a particular survey station in a particular wellbore.

The actual survey inclination and azimuths are obtained from the sensor data via a set of survey equations. So for example for a standard MWD tool the inclination and azimuth are determined from the following equations:

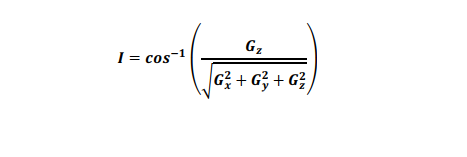
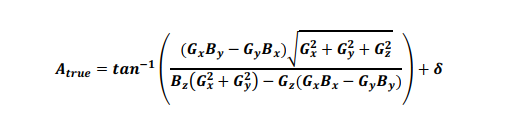
Similar survey equations exist for gyros tools and these MWD equations change if axial interference corrections are made.

The weighting functions can be derived from these equations by taking the partial derivatives of the survey equations with respect to the error source. Examples of the derivations can be found in the SPE papers, whilst all of the error sources and weighting functions for both models are given in the appendices. We now consider another example to illustrate this point:

Example 2: Sensor error – Z-Accelerometer Bias
If we consider the effect of a z-accelerometer bias error; instead of reading the correct value of the tool will actual give:

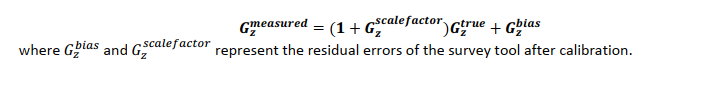
This equation represents a fairly standard, first-order method for modelling the output of a sensor (almost any type of sensor), when we know that it will not give perfect output.

The MWD model has an error source, coded ABZ for the z-accelerometer bias which corresponds to this bias term. From the MWD survey equations above, we can see that the Gz term appears in both the inclination and azimuth equations.

However, the accelerometer readings don’t have any effect on measured depth. So the MD weighting function is 0, but the inclination and azimuth weighting functions are determined by taking the partial derivatives of these survey equations with respect to Gz i.e. for ABZ the weighting functions are:

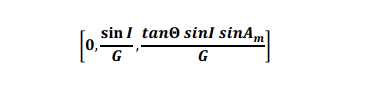
Since we are assuming that this z-accelerometer bias is due to residual tools errors, this error source will have the same value for each survey taken with that tool. However, if we change tools, the error will change. Hence the propagation mode is systematic (the same at each survey station in a run, but different for different legs and wells).

The model gives ABZ a magnitude of 0.004 ms-2, meaning that for a number of properly calibrated tools if we ran a number of tests, we’d expect to get a Gaussian distribution of results with a standard deviation of 0.004 ms-2.

Gyro tools can be designed a little differently – some systems also have a cluster of three accelerometers and the inclination weighting function will be the same as the MWD case (this is the gyro AXYZ-ZB term). Other gyro tools only have x and y-accelerometers and use the assumed total gravity value, and therefore these tools would be modelled without a z-accelerometer bias term. We can see that the error sources which are included in any particular survey tool model depend on the design of that tool.