A key point to remember is that the projection central meridian is truly a meridian – there is no azimuth distortion. As one moves away from the central meridian east or west, the other meridians plot on the projection as curved lines that curve towards the nearest pole, whereas grid north lines are parallel to the central meridian. At any given point, the difference in azimuth between the grid north lines and the meridian lines is the convergence angle. On the equator, convergence is generally zero also, and increases as one moves north.
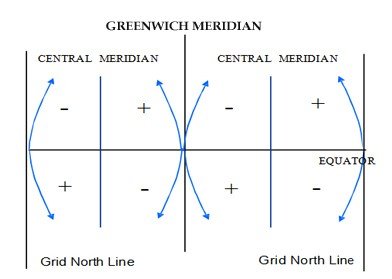
Above shows a simple way to verify that the value derived is correct (i.e. that the sign of convergence has been correctly applied). It is important when dealing with convergence to do a couple of ‘sanity’ checks:
- Always draw a diagram
- Always check that the software application is applying the correct value, correctly
- Always have someone else check that the results agree with supplied results of wellbore location
- If you are not sure – find a specialist
The formal algorithm is Grid azimuth = True Azimuth – Convergence but many applications do not observe the correct sign. It is better to use True Azimuth = Grid Azimuth ± Convergence α where (per figure 19), α -ve West of CM, and α +ve East of CM in Northern hemisphere and the opposite in Southern hemisphere.
In the equation above, use the sign in the diagram, not the sign you get with the software, because some applications use the opposite convention.


Post your comment on this topic.