18.2 Covariance

First we have to introduce the idea of “covariance”.

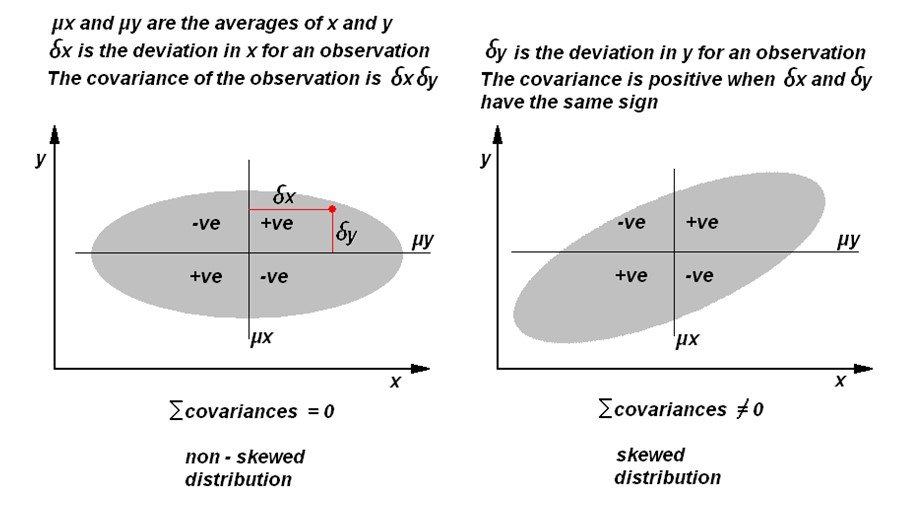
As the name suggests it is a measure of how parameters vary together. Recall that we discussed how height and weight might vary together (correlate) but height and intelligence do not. If we measure the variance of an observation it is simply the square of the deviation but the covariance is the product of the deviations of two parameters. The covariance helps us to measure the correlation which shows up as a “skew” in the ellipse.

The figure above shows this, but it is also true in 3D and if we can build up a matrix of covariances in northings, eastings and TVD we can derive an ellipsoid, its dimensions and orientation in 3D space.

In order to build up this matrix we need to know how each error source affects the observations and how the observation error will move the wellpath in North, East and vertically in TVD.