1.2.1 Geodesy

Geophysics and Geology – is a study of the Earth. We use models as the other two disciplines do, and make adjustments for distortion and errors in those models.

Geodesy provides the ‘frame of reference’ for all good maps. It is the means by which we can put together all sorts of different data attributes and ensure that they are correctly juxtaposed. So while we are interested in the relative position of one piece of data to another, the means by which this is achieved is through providing an ‘absolute’ framework or set of rules that ensures that we can do this correctly. Geodesy is rightly then to be considered the underlying and immutable doctrine required to ensure that maps (the cartographers ‘art’) properly represent the real world they are designed to portray.

Geodesy is defined as the study of:

• the exact size and shape of the Earth
• the science of exact positioning of points on the Earth (geometrical geodesy)
• the impact of gravity on the measurements used in the science (physical geodesy)
• Satellite geodesy, a unique combination of both geometrical and physical geodesy, which uses satellite data to determine the shape of the Earth’s geoid and the positioning of points.

Let us return to the ellipsoid that we studied in the previous section (below). This time, I have ‘cut away’ a quadrant of the ellipsoid so we can see the centre. On this diagram we can see two coordinate systems. One is the Latitude, Longitude and Height of a point ‘P’ in space above the ellipsoid surface (it could just as well be below). The other is a three dimensional Cartesian coordinate system where X is in the direction of the Greenwich meridian in the equatorial plane, Y is orthogonal to the Greenwich meridian and Z is parallel to the polar axis (orthogonal to the other two axes). The Cartesian system is directly referenced to the ellipsoid centre, the geographic system is directly referenced to the ellipsoid surface and indirectly to the ellipsoid centre. However, both systems are valid and both describe in different ‘numbers’ the coordinates of the point ‘P’.

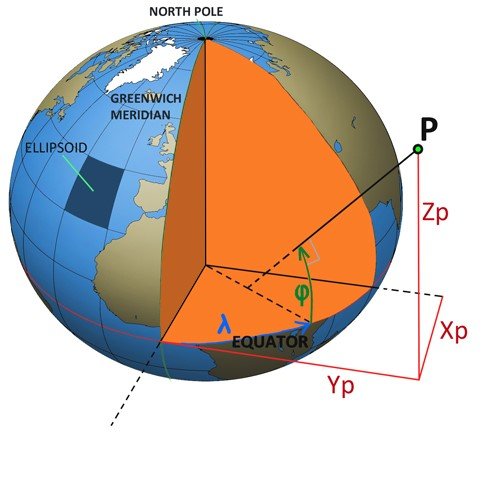
The relationship between the two systems is per the following algorithms:

X = (ν + h) * cos φ * cos λ
Y = (ν + h) * cos φ * sin λ
Z = [(b2 * ν/a2 ) + h] * sin φ

(where ‘ν’ is the radius of the ellipsoid at P).