1.2.3 Distortions in the Ellipsoidal Model

As the reader will have surmised, the ellipsoidal model is not an exact fit. The larger the area covered by a datum, the more distortion there is.

Height and Elevation – the elevation above MSL is not the same generally as the height above the ellipsoid. Corrections must be made to GPS or other satellite derived ‘heights’ to adjust them to mean sea level. Measurements made and adjusted to mean sea level by the surveyor may be assumed to lie on the ellipsoid as long as the separation between the two surfaces is relatively small.

Related to the previous one, the direction of the local vertical is not the same as the normal to the ellipsoid. This difference is known as the ‘deflection in the vertical’ and has to be minimized especially across larger regional and continental datums. This is done using Laplace corrections at regular intervals across the area of interest. Since these corrections vary in a non-regular and non-linear manner, the datum transformation between two datums may vary significantly across larger datums. The EPSG database is a means of identifying where a particular set of parameters should be used.

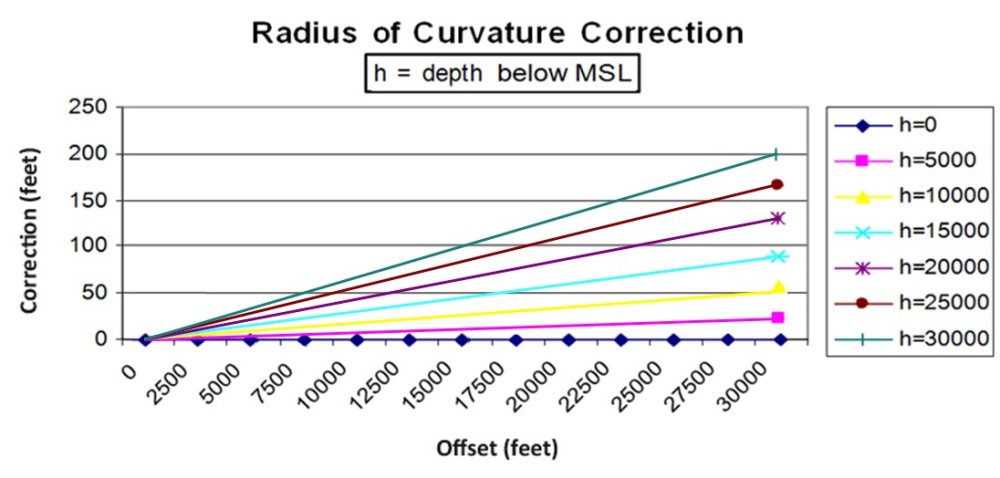
Radius of curvature adjustment (below) – The ellipsoid has a radius of curvature at a point (varies across the ellipsoid). When measuring distances at heights above or below the ellipsoid of more than about 5000 ft, the distances need to be adjusted to allow for the change in radius of curvature, so that they ‘map’ correctly onto the ellipsoid. Measurements made above the ellipsoid need to be reduced and measurements made below the ellipsoid need to be increased respectively, so that a map of the area (computed at the ‘true’ ellipsoid radius) map correctly onto the map in relation to other features. The calculation can be made with the following equation:

Ellipsoidal length = d[1 –( h/(R + h))]
where
d = measured length
h = mean height above mean sea level (negative if below)
R = mean radius of curvature along the measured line

Section summary

The most important lesson from all this is that a latitude and longitude coordinate do not uniquely define a point in space unless the datum name is included as part of the description! Please also note that knowing the name of the ellipsoid is not enough. An ellipsoid is a shape in space and the same ellipsoid can be attached to the Earth at an infinite number of places. Each time an ellipsoid is attached to another place it represents a different datum. Particular examples occur in West Africa, where many countries use the Clarke 1880 ellipsoid but set up as a different astro-geodetic datum in each case, and in Brazil where three datums use the International ellipsoid of 1924.

Ten Things to Remember about Geodesy and References:

1. Latitude and Longitude are not unique unless qualified with a Datum name.
2. Heights/Elevations are not unique unless qualified with an height/elevation reference.
3. Units are not unique unless qualified with unit reference.
4. Orientations are not unique unless qualified with a heading reference.
5. Most field data of all types are acquired in WGS 84 using GPS.
6. Every time data are sent somewhere there is a chance someone will misinterpret the references.
7. Most datasets have an incomplete set of metadata describing the references.
8. All software applications are not created equal with respect to tracking and maintaining metadata.
9. Data can be obtained by anyone from anywhere – that doesn’t make it right!
10. Most people do not understand geodesy – if you are in doubt – check with someone who knows!