1.1 The Origin – Reference Surfaces and Elevations in Mapping

The Origin – Reference Surfaces and Elevations in Mapping

There are three basic surfaces that are pertinent to good mapping, shown here, these are:

Terrain: The topographic surface of the ground or seabed

Geoid: An equipotential surface that is irregular and approximates to Mean Sea Level (MSL)

Ellipsoid: A regular model surface that approximates the geoid, created by rotating an ellipse about the polar axis. Used to simplify the computational complexity of the Geoid

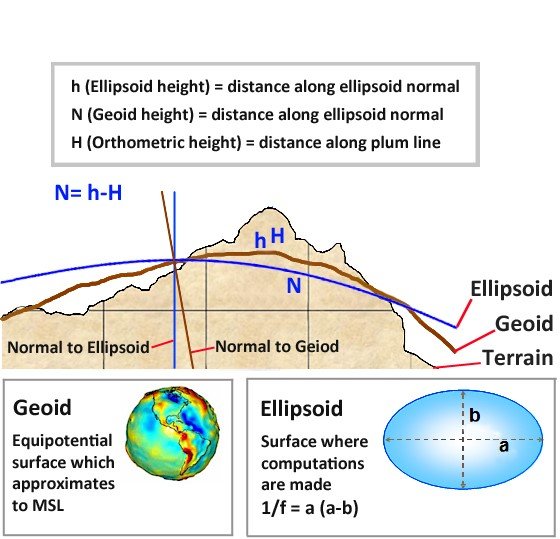
Terrain: The terrain is the surface we walk on or the seabed. This surface is irregular. It is the surface we have to set up our survey measuring devices, such as a ‘total station’ or a GPS receiver. The nature of the surface will dictate the direction of gravity at a point. In mountainous terrain, the vertical will deflect in towards the main ‘centre of mass’ of the mountains.

The Geoid: The equipotential surface of the Earth’s gravity field which best fits, in a least squares sense, global mean sea level (MSL). An equipotential surface is a one where gravity is an equal force everywhere, acting normal to the surface. The geoid is an irregular surface that is too complex for calculation of coordinates.

The Ellipsoid: The ellipsoid is a ‘model’ of the Earth that permits relatively simple calculations of survey observations into coordinates. The ellipsoid provides the mathematical basis of geodesy. Note that the Geoid is an ‘actual physical surface like the terrain, but the ellipsoid is a ‘theoretical’ surface that is designed to ‘match’ the geoid as closely as possible in the area of operations. Note also that the normal to the geoid (which is ‘vertical’) is not the same as the normal to the ellipsoid.

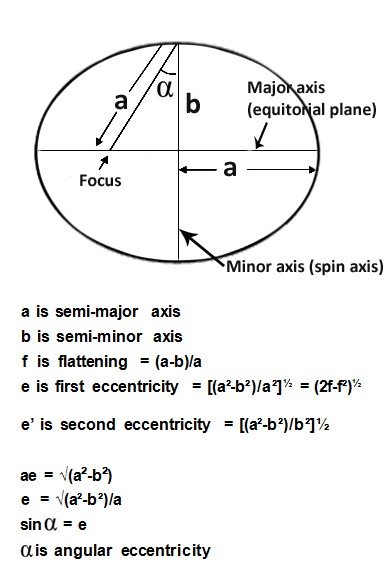
An ellipsoid is created when an ellipse is rotated around its polar axis. The ‘mathematical’ properties of an ellipse are shown below. ‘a’ is assigned to represent the semi-major axis or equatorial radius and ‘b’ the semi-minor or polar axis. The flattening, ‘f’, equals the ratio of the difference in ‘a’ and ‘b’ over ‘a’.