17.3 Probability in two dimensions

Something interesting happens when we try to guess two parameters at the same time and still need to be confident of our estimates. Let’s say we now guess the person’s height and their intelligence. First, it is important that we understand that these parameters are not “correlated”. In other words, despite what your taller friends might like to think, there is no relationship between height and intelligence. If we were measuring height and weight, we might expect some “correlation” since taller people are probably going to be heavier than shorter people in general.

Watch what happens when we plot the normal distribution curves for the two parameters at once. In this diagram I have drawn the distribution curves on IQ for two height groups on either side of average height. Note that the average IQ for the small group is the same as the average IQ for the tall group.

This demonstrates no correlation between height and intelligence. The average intelligence of all height groups remains the same.

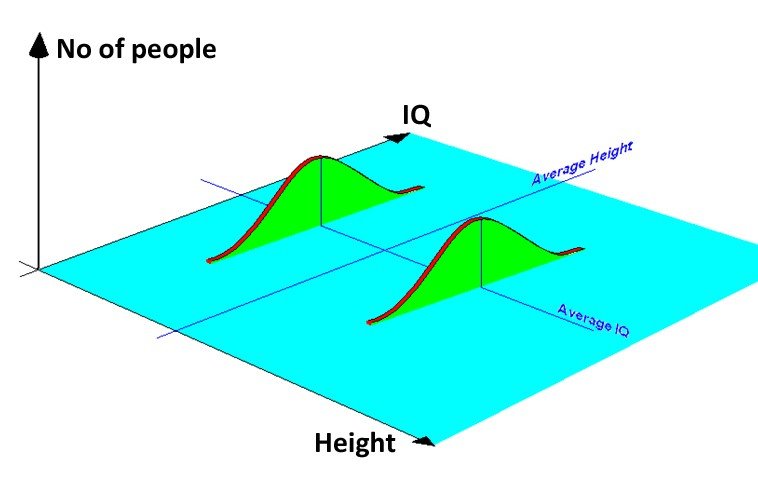
Now we shall plot all the normal distributions for all the height groups.

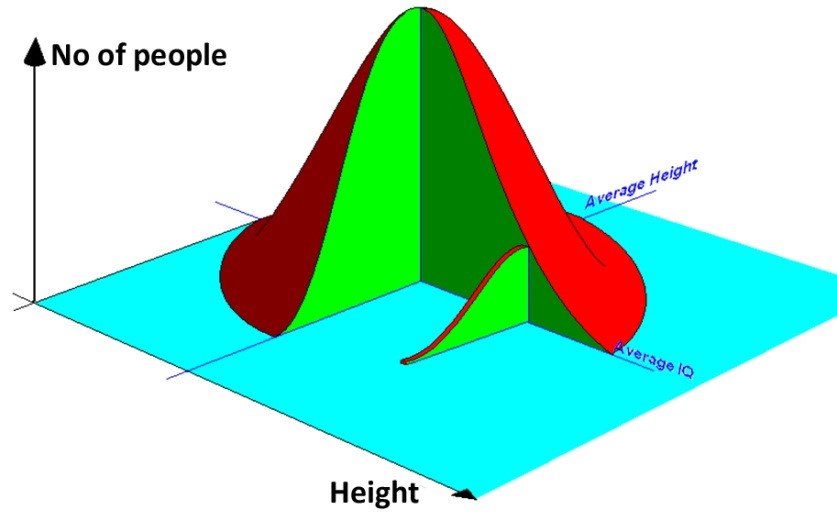
This normal distribution “mountain” describes the probabilities of two parameters whose ranges are not the same. Any probability “contour” on the slopes of this mountain will therefore be elliptical in shape since the IQ range and the height range have different values.

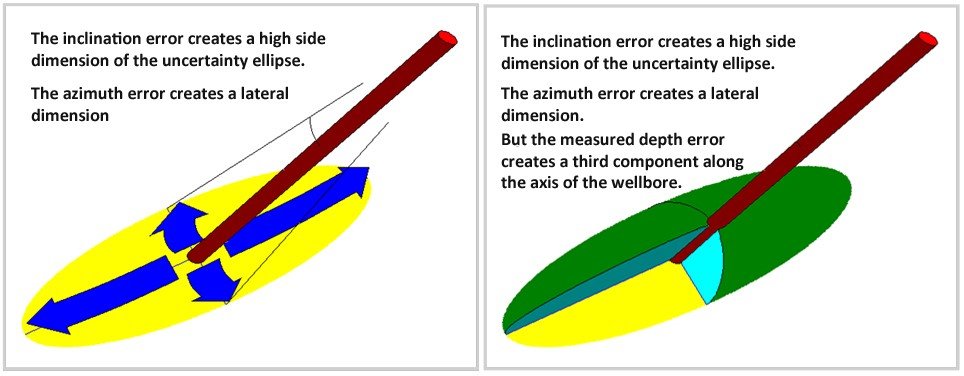
Now we shall apply this to a section of wellbore. Let us imagine that the well section is straight and has an inclination “I” and an azimuth “A” but both are potentially in error.

An ellipse of uncertainty is formed around the wellbore where the lateral dimension is proportional to the azimuth error and the high side dimension is proportional to the inclination error. If the azimuth was more accurate than the inclination, the ellipse would be thinner across the wellbore. This example is more typical with the azimuth less certain than the inclination, creating an ellipse with a larger lateral dimension. The final shape is like an almond, elliptical in all three orthogonal planes.